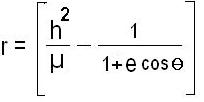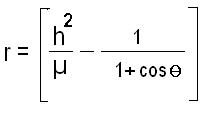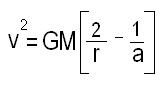What is the orbital energy conservation equation for hyperbolic trajectory?
The specific orbital energy (ϵ) of a hyperbolic trajectory is greater than zero.
The orbital energy conservation equation for hyperbolic trajectory is given as,
∈ = µ / -2a
∈ = specific orbital energy
µ= is the standard gravitational parameter
a = the length of the semi-major axis (a > 0 for ellipses, a = ∞ or 1/a = 0 for parabolas,
and a < 0 for hyperbolas)