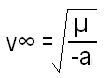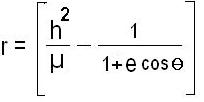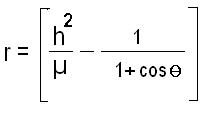In orbital mechanics, Kepler’s equation relates various geometric properties of the orbit of a body subject to a central force.
The formula Kepler’s equation for calculating orbits is given as,

M = E – ϵ sin E

M = the mean anomaly
E = the eccentric anomaly
ϵ = the eccentricity

It is a transcendental equation because sine is a transcendental function. It means that it cannot be solved for E algebraically. Numerical analysis and series expansions are generally required to evaluate E.

A body traveling along hyperbolic trajectory will attain in infinity an orbital velocity called hyperbolic excess velocity (v_∞).

The formula for Hyperbolic excess velocity is given as,

v_∞ = √〈µ / -a〉

v_∞  = Hyperbolic excess velocity

µ  = is the standard gravitational parameter

a = the length of the semi-major axis (a > 0 for ellipses, a = ∞ or 1/a = 0 for parabolas,

                                                                   and a < 0 for hyperbolas)

The specific orbital energy (ϵ) of a hyperbolic trajectory is greater than zero.

The orbital energy conservation equation for hyperbolic trajectory is given as,

∈ = µ / -2a

∈ = specific orbital energy

µ= is the standard gravitational parameter

a = the length of the semi-major axis (a > 0 for ellipses, a = ∞ or 1/a = 0 for parabolas,

                                                            and a < 0 for hyperbolas)

In astrodynamics or celestial mechanics a hyperbolic trajectory is a Kepler orbit with eccentricity greater than 1.
The orbit formula Hyperbolic orbits is,

r = the radial distance of the orbiting body from the mass center of the central body

h = specific angular momentum of the orbiting body

µ  = is the standard gravitational parameter

Ɵ = the true anomaly of the orbiting body

e = eccentricity

In astrodynamics or celestial mechanics a parabolic trajectory is a Kepler orbit. It eccentricity is equal to 1. When moving away from the source it is referred to as an escape orbit, otherwise a capture orbit.

The equation or formula for Parabolic orbits is,

r = the radial distance of the orbiting body from the mass center of the central body

h = specific angular momentum of the orbiting body

µ = is the standard gravitational parameter

Ɵ = the true anomaly of the orbiting body.