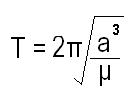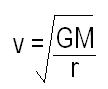What is the orbital speed of a body traveling along an elliptic orbit?
In astrodynamics, the orbital speed of a body traveling along an elliptic orbit can be computed from the orbital-energy-invariance law. It is one of the equations that model the motion of orbiting bodies.
Under standard assumptions the orbital speed (v) of a body traveling along an elliptic orbit is computed from the orbital-energy-invariance law as,
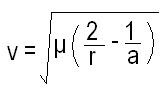
v = orbital speed of a body traveling along an elliptic orbit
μ = is the standard gravitational parameter
r = the distance between the orbiting bodies
a = the length of the semi-major axis