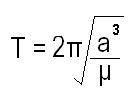In astrodynamics, the orbital speed of a body traveling along an elliptic orbit can be computed from the orbital-energy-invariance law. It is one of the equations that model the motion of orbiting bodies.

Under standard assumptions the orbital speed (v) of a body traveling along an elliptic orbit is computed from the orbital-energy-invariance law as,

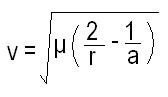
v =  orbital speed of a body traveling along an elliptic orbit

μ = is the standard gravitational parameter

r = the distance between the orbiting bodies

a = the length of the semi-major axis

The orbital period is the time taken for a given object to make one complete orbit around another object. It is applicable in astronomy.

The orbital period T (in seconds) of two bodies orbiting each other in a circular or elliptic orbit is given as,

Where,

μ = G × M

G is the gravitational constant,

M is the mass of the more massive body.

a = the orbit’s semi-major axis in meters

μ = the standard gravitational parameter in m³/s²

All bounded orbits where the gravity of a central body is strong are elliptical in nature. An example of this is the circular orbit, which is an ellipse of zero eccentricity.

The formula for the velocity of a body in a circular orbit at distance r from the centre of gravity of mass M is given as,

To properly use this formula, the units must be consistent – M must be in kilograms, and r must be in meters

v = velocity

G = gravitational constant

M = mass of the body

r = distance from the centre of gravity of mass M

Orbits are conic sections so the formula for the distance of a body for a given angle is given as,

r = ƿ / (1 + ecosƟ)

where,

ƿ = h² / µ

µ= called the gravitational parameter

h = the specific angular momentum of object 2 with respect to object 1

Ɵ = known as the true anomaly

ƿ = the semi-latus rectum

e = the orbital eccentricity

The specific energy (energy per unit mass) of a space vehicle is composed of two components, the specific potential energy and the specific kinetic energy.

The specific orbital energy of two orbiting bodies is the constant sum of their mutual potential energy and their total kinetic energy, divided by the reduced mass.

The formula for specific orbital energy is given as,

specific orbital energy = specific kinetic energy + specific potential energy

ϵ=ϵ_{k +} ϵ_p

We know value of

ϵ_k= v² / 2 ——  where ϵ_k = specific kinetic energy  and v = velocity .

and
ϵ_p = − GM / r  ——  where   ϵ_p = specific potential energy , G = the universal gravitational constant   ,  M = the mass of the body to be escaped and r = distance from the centre of mass of the body to the object.

Therefore,

ϵ= (V² / 2)–(GM / r)

ϵ = specific orbital energy.

v = velocity

G = the universal gravitational constant (G = 6.67×10−11 m3 kg−1 s−2)

M = the mass of the body to be escaped

r = distance from the centre of mass of the body to the object.